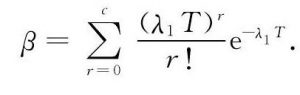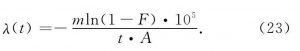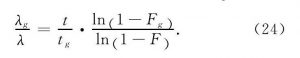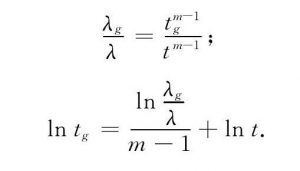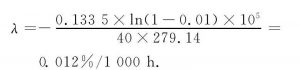固体电解质钽电容器失效率鉴定

电容器失效率鉴定方法包括指数鉴定和威布尔鉴定两种, 其中指数鉴定法的适用范围更广, MIL-STD-690C-1993, GJB 2649—1996对其抽样方案和程序作出了详细规定, 而威布尔鉴定法仅用于固体电解质钽电容器的失效率鉴定, 在固体电解质钽电容器对应的国军标总规范中, 有相关的详细规定。虽然GJB 2283—1995和GJB 63B—2001同时规定了固体电解质钽电容器的两种失效率等级 (指数分布鉴定失效率等级M, P, R, S和威布尔鉴定失效率等级B, C, D) , 但目前航天型号所使用的均为采用指数鉴定的固体电解质钽电容器。目前, 国内关于指数分布和威布尔分布用于元器件失效率鉴定的研究主要通过公式推导, 结合不同元器件的固有特点验证这两种鉴定方法的正确性及可行性。但因与元器件固有的特点紧密结合, 使推导局限于某一类型的元器件, 而且对指数鉴定和威布尔鉴定的研究通常各自独立, 国内目前尚无文献对两种方法进行比较。本文对固体电解质钽电容器指数分布和威布尔分布失效率鉴定方案进行了研究。

对基于指数分布的建模, 钽电容器失效分布函数

式中:λ为钽电容器的失效率。

钽电容器对应的可靠度

固体电解质钽电容器抽样检验一般需要有很大数量的抽样数n。当n只样品中不合格数为r时, 样品合格数为n-r, n只样品中出现r只不合格品的概率

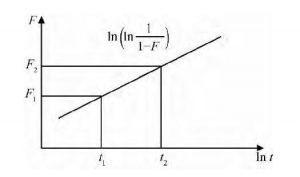
若允许的不合格品数为c (r

将式 (1) 、 (2) 代入式 (4) , 得

由于失效率鉴定中λ很小, 有

将式 (6) 代入式 (5) , 可得

因失效率鉴定中r很小, 而n又很大, 故总试验时间T可近似表示为

将式 (9) 代入式 (8) , 可得

假设固体电解质钽电容器鉴定合格的最低失效率λ_1＜λ, 同时λ₁对应的风险β (置信度为1-β) 为

根据文献, 对用部分积分法反复计算右边积分, 证明其等于式 (10) 。

在总试验时间为T的失效等级鉴定试验中, 发生失效不超过r的概率可用Γ函数表示为

为将L (λ) 化成卡方分布, 以便在实际使用时直接查表, 设2t=x, 2 (c+1) =f, 则有

式 (13) 即为自由度为f的卡方分布。此处:β为所选择的接受概率。故有

根据式 (14) , 选择不同的β (如10%, 40%, 90%) , 即可求得与不同失效数c值对应的T值, 最终可得GJB 2649—1996的一次失效率抽样方案表格。如某M级产品的置信水平90%, 最大失效率1%/1 000h, c=2 (即自由度2 (c+1) =6) , 查卡方分布分位表得1.064, 则

由于每次鉴定所需的n很大, 周期也较长, 因此指数鉴定方法不适于逐批对钽电容器进行失效率维持鉴定。GJB 2283—1995和GJB 63B—2001将失效率鉴定的维持置于周期试验中, 规定每3个月进行一次。又因置信度越高, 试验时间和成本的增幅越大, 故国军标将维持失效率鉴定的置信度定为10% (即接受概率β=90%) 。这是一种较宽松的鉴定模式。采用该方法进行维持鉴定, 须保证生产过程的稳定性, 即试验批能大致代表周期内所生产的产品的情况。

另外, 用指数鉴定法进行鉴定时, 如需将产品失效率升级到S级, 需要极其大量的元件小时数的累积, 因此指数分布的失效率鉴定适于超大批量生产的产品。虽然GJB 2649—1996规定, 在升级到R级和S级时, 可组合一个型号中结构相似的两个或多个电压组累积数据, 但这仍需耗费很长时间。就目前国内的情况来说, 因为规格数、产量和生产的时间都远不及国外, 国军标固体电解质钽电容器最高失效率等级仅达到P级。

在产品使用过程中, 其寿命服从的分布函数用F (t) 表示, 在寿命区间, 不失效函数即产品的可靠度R (t) =1-F (t) 。对产品的失效密度f (t) , 有。假设产品的失效率为λ (t) , 则有

在威布尔分布中, 有

式中:m为形状参数;为位置参数;η为真尺度参数 (特征寿命) 。

在固体电解质钽电容器的失效率鉴定方案中, 式 (16) 作图回归后成线性, 故γ=0[1]。可将式 (16) 化为

对式 (19) 作变换, 得

-lnη, 代入式 (20) , 有

利用线性回归法作直线, 如图1所示。该直线的斜率A=m, 直线在y轴的截距为-lnη。

威布尔分布的失效率鉴定时, 可通过改变电压应力, 在一个可行的时间限度内达到数千小时的等效试验值。因为改变电压应力, 故在表示电压和产品寿命关系时, 符合电压逆幂定律式中:A为加速因子;α, β为与应力无关的常数;V_c, V_r为加速电压和额定电压[2]。

得到A后, 式 (18) 可改为

变换式 (19) , 可得, 代入式 (22) , 同时为使失效率能用1 000h的百分比表示, 增加10⁵因子, 可得新的失效率

由式 (23) 可得试验进行t小时后的钽电容器失效率。如需得到某一更高失效率λ_g, 则所需的试验时间满足

用式 (19) 对式 (24) 中ln (1-F_g) , ln (1-F) 进行代换, 得

例:使用1.3倍额定电压, 对300只片式固定钽电容器进行威布尔失效率鉴定。2h后进行第一次失效计算, 有2只失效;40h试验结束时, 又发现一只失效。

根据GJB 63B—2001规定, 使用1.3倍额定电压时, 加速因子为279.14, 则F₁=2÷300=0.67%, F₁=3÷300=1%。

根据式 (20) 画出典型失效率曲线, 并求得斜率m=0.133 5。将m值代入式 (23) , 得

0.01%/1 000h

综上所述, 用威布尔分布的失效率鉴定法可实现对产品的逐批鉴定。相应地, GJB 2283—1995, GJB 63B—2001将威布尔分布产品的失效率鉴定放在A组逐批检验进行。由于每批产品都进行鉴定, 而且为保证不同批次产品的一致性, 接受威布尔定级的产品须达到指数分布鉴定的P级, 这样得出的产品的失效率等级非常可信。另外, 由于采用逐批鉴定的方式, 威布尔分布的失效率鉴定无需通过大量的元器件小时累积升级失效率, 即在小批量供货情况下用威布尔鉴定法仍能准确地鉴定产品的失效率等级。因此, 该方法非常适合航天需求。但用威布尔分布对固钽电容器进行失效率鉴定还存在技术难点。由上述计算可知, 欲取得较好的鉴定效果, 须将电压应力控制在额定电压的1.3~1.5倍, 为此须对产品生产过程进行更严格的控制。目前国内主要的军工钽电容器制造厂商, 筛选电压一般控制在1.0~1.2倍的额定电压, 只有少量供航天用的元件能将筛选电压控制在1.4倍额定电压。

由两种鉴定方法的原理可知, 指数鉴定属周期鉴定方式, 每3个月进行一次鉴定的维持;威布尔鉴定属逐批鉴定方式, 可用于对每批产品进行鉴定。相对来说, 前者更适于整个生产工艺和生产线稳定性的考核, 而对周期内生产的每批产品的可靠性差异, 其鉴定结果往往不够准确, 后者可对同一生产线生产的不同批次的产品进行鉴定, 使每批产品都有其对应的失效率等级;考虑生产工艺和生产线的稳定性, 威布尔鉴定必须在生产线达到指数分布的P级后才能进行。MIL-PRF-39003固体电解质钽电容器通用规范中规定, 可用威布尔分布失效率B级 (0.1%/1 000h) 产品替代指数分布失效率S级 (0.001%/1 000h) 的产品, 这充分证明了威布尔分布失效率鉴定的准确性和可靠性。

另外, 两种鉴定方法的适用场合不同。指数分布的失效率鉴定方法因失效率等级提升需大量元件小时数的累积, 适于大批量生产的产品, 而威布尔分布的失效率鉴定方式的失效率等级可通过对每一批产品的鉴定而得, 且因加速因子的存在, 鉴定周期不致过长, 故非常适于小批量生产的高质量等级产品。

通过两种失效率鉴定方法的比较, 可知对航天用固体电解质钽电容而言, 威布尔分布的失效率鉴定方法具有更好的适用性, 与指数分布的失效率鉴定方式相比, 能够更准确地表征产品的固有可靠性。航天用固体电解质钽电容既要满足高失效率等级要求, 又非大批量生产产品, 无疑应采取威布尔分布的失效率鉴定方式。
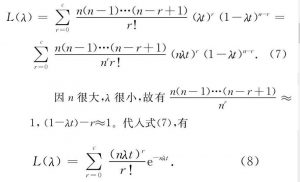